Map Projections
What are map projections?
A map projection is a transformation of the locations on a sphere or ellipsoid into locations on a plane. The mathematician Carl Friedrich Gauss proved in the nineteenth century that a sphere’s surface cannot be projected onto a flat plane without distortion. The same holds true for other curved surfaces like ellipsoids. So any map projection introduces distortion. Different map projections have different distortion properties. As there is no perfect way to transform a globe into a plane, several methods were invented, all with their own compromises.
What properties do map projections have?
A map can’t preserve all of the metric properties such as angles, areas and distance. Thus map projections are classified by the metric properties they preserve.
- Conformal: Map projections that preserve angles locally are called conformal. Small shapes on the earth are displayed in a similar shape on the map.
- Equal-area: Equal-area maps preserve area measure. Any two figures on earth having the same size have the same size on the map. In order to achieve this, equal-area maps are distorted, especially near the edge of the map.
- Equidistant: Equidistant map projections don’t preserve distance between any two points, but just from some standard point or line. They also distort the shape of the projected areas.
- Compromise: Not all projections try to preserve a metric property. Several projections seek a balance between the possible distortions and try to “look right”.
What kind of projections are typically in use today?
Here you see maps using the projections that are typically in use today.
Mercator Projection
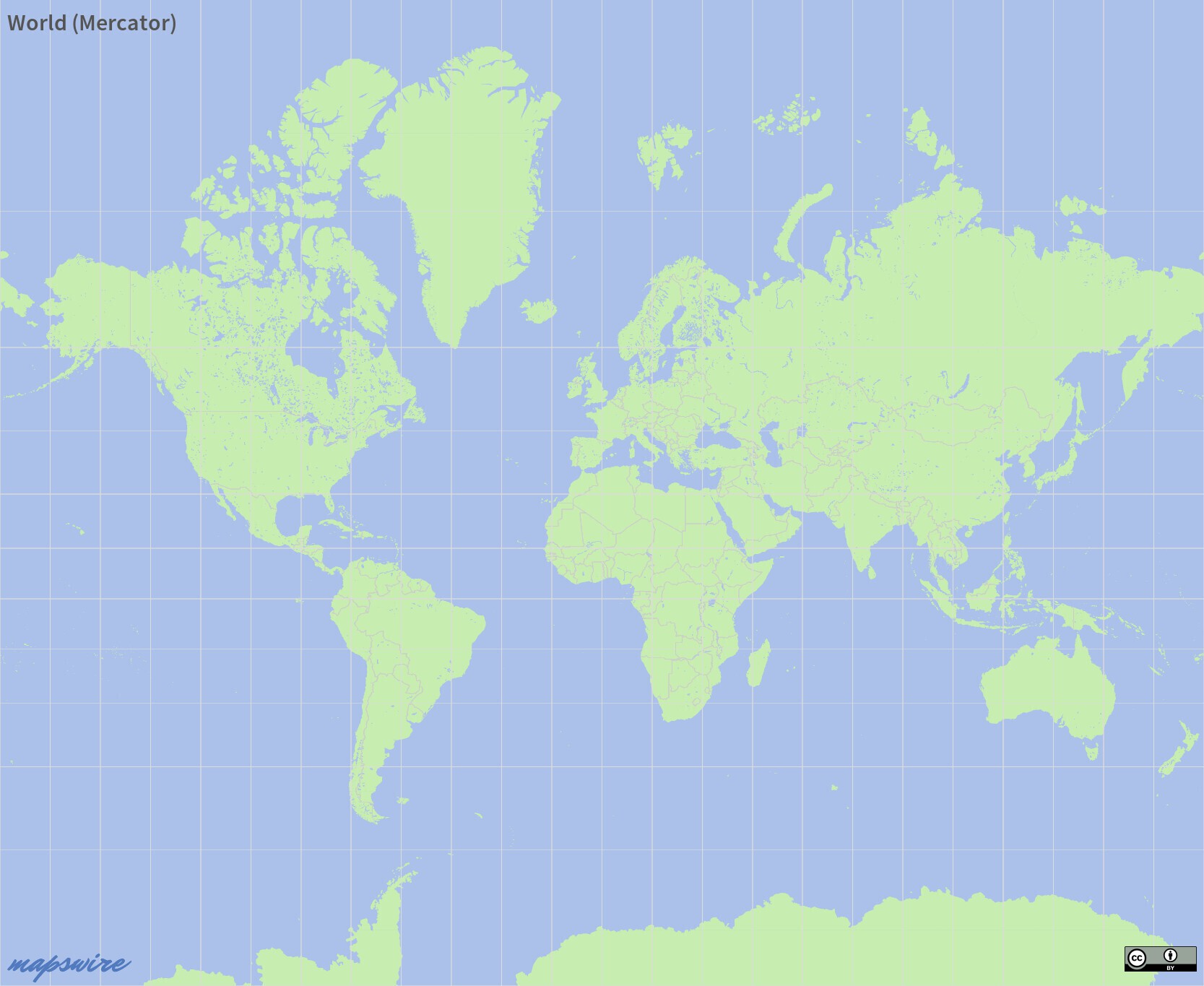
Introduced in the sixteenth century the Mercator Projection is still in widespread use today. As a conformal projection it preserves the look of smaller shapes. Lines of constant bearing are straight on Mercator maps, so they are used as navigation aids. The big downside of Mercator is that areas are inflating with latitude. On a Mercator map Greenland looks nearly as big as Africa, while in reality Africa has about 14x the size of Greenland. A simplified variant of Mercator (called Web Mercator) introduced by Google is the de-facto standard for web mapping, being used by Google Maps, Open Street Maps or Bing Maps.
Miller Projection
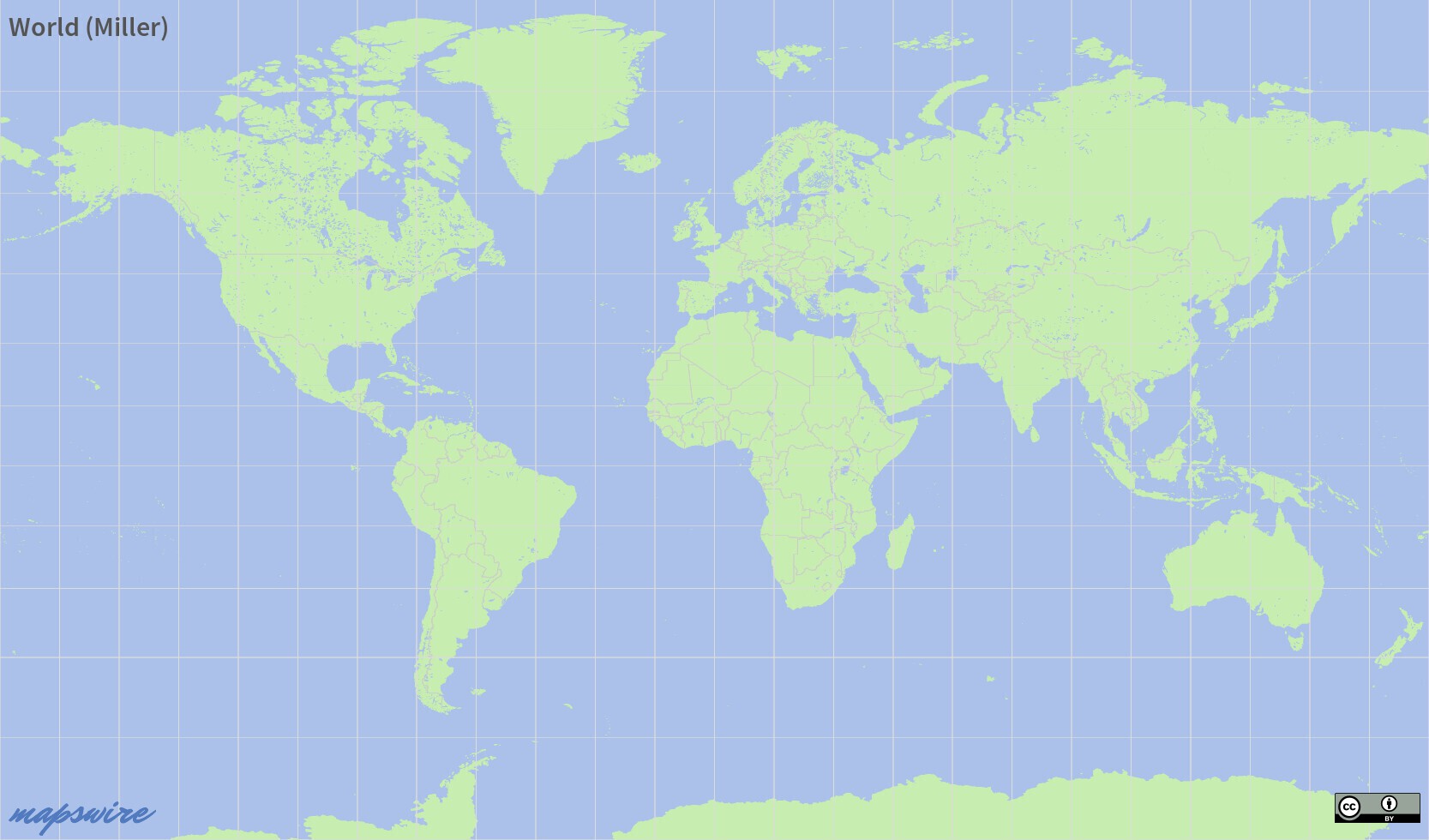
The Miller projection is a modified Mercator projection. The inflation of areas near the poles is reduced, so Miller maps look rather similar to Mercator maps without the extreme size distortions in northern and southern regions. Because of these compromises, Mapswire.com uses Miller projection as its standard projection for most of its maps.
Robinson Projection
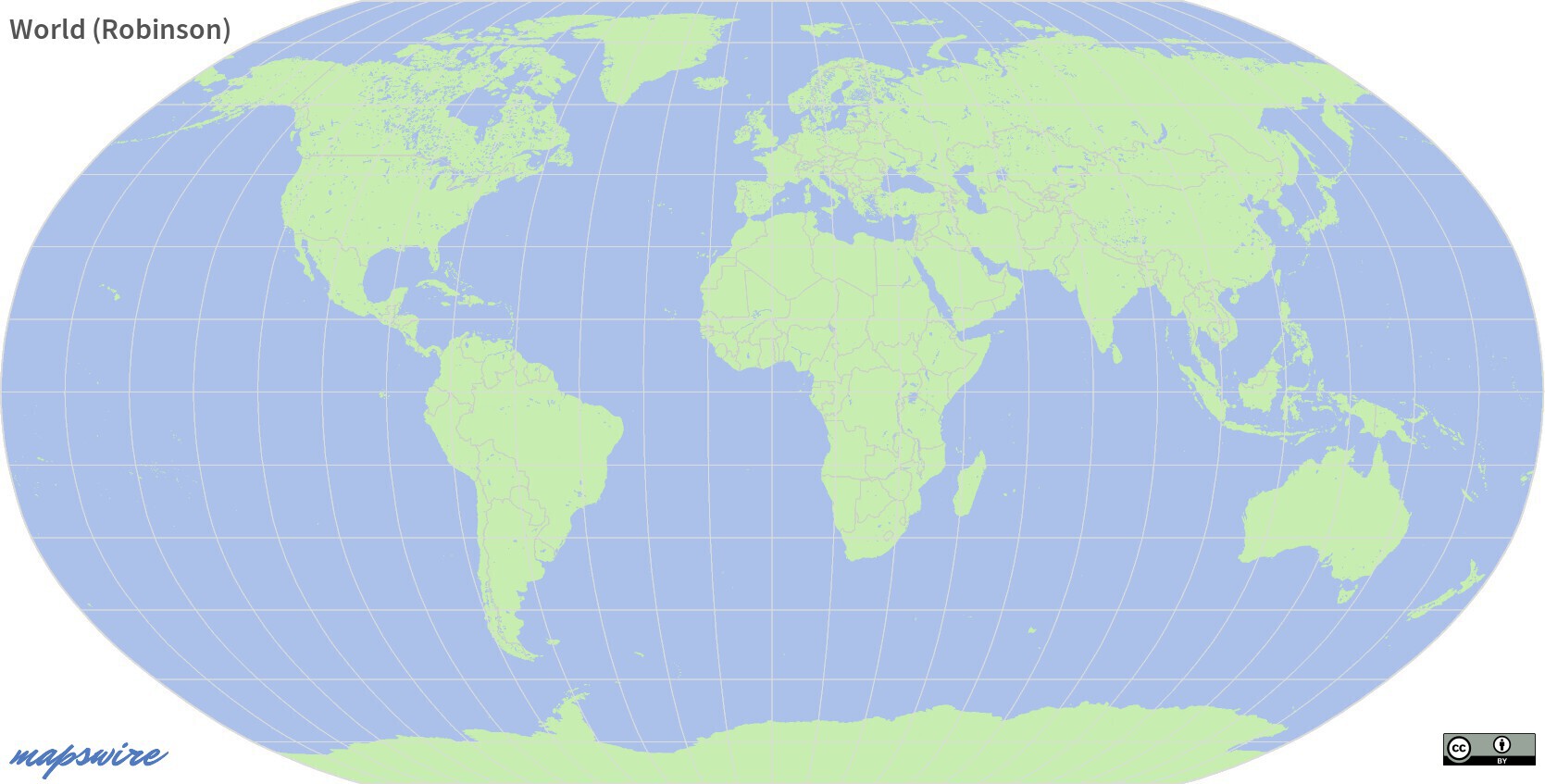
The Robinson projection is another compromise projection. Size distortions are further reduced at the cost of increased shape distortions.
Mollweide Projection
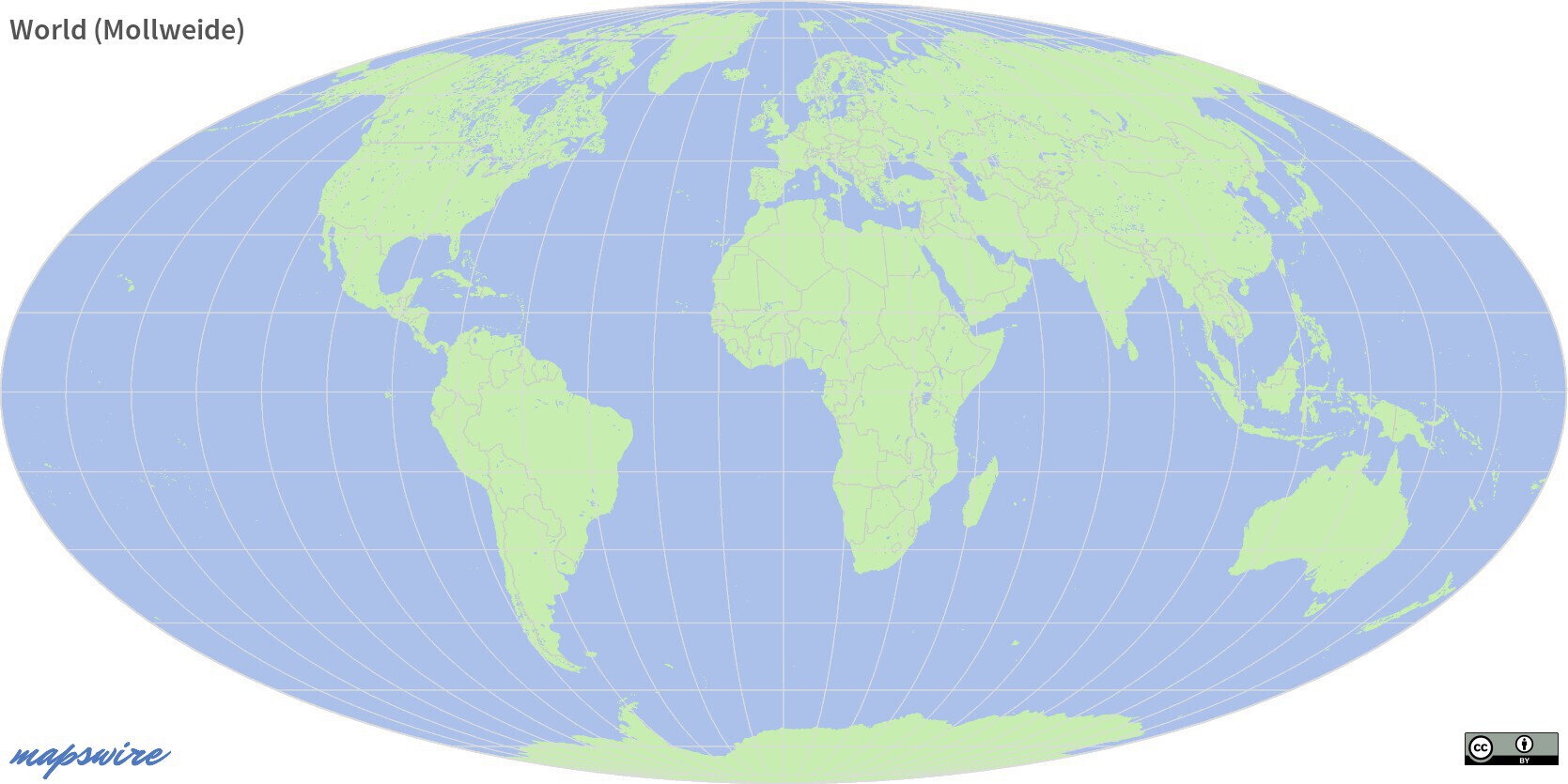
The Mollweide projection is an equal-area map projection. It preserves the size of figures, but heavily distorts the shapes when getting nearer to the edge of the map. Mollweide maps are especially used for global maps where its equal-area property helps to display global distributions.
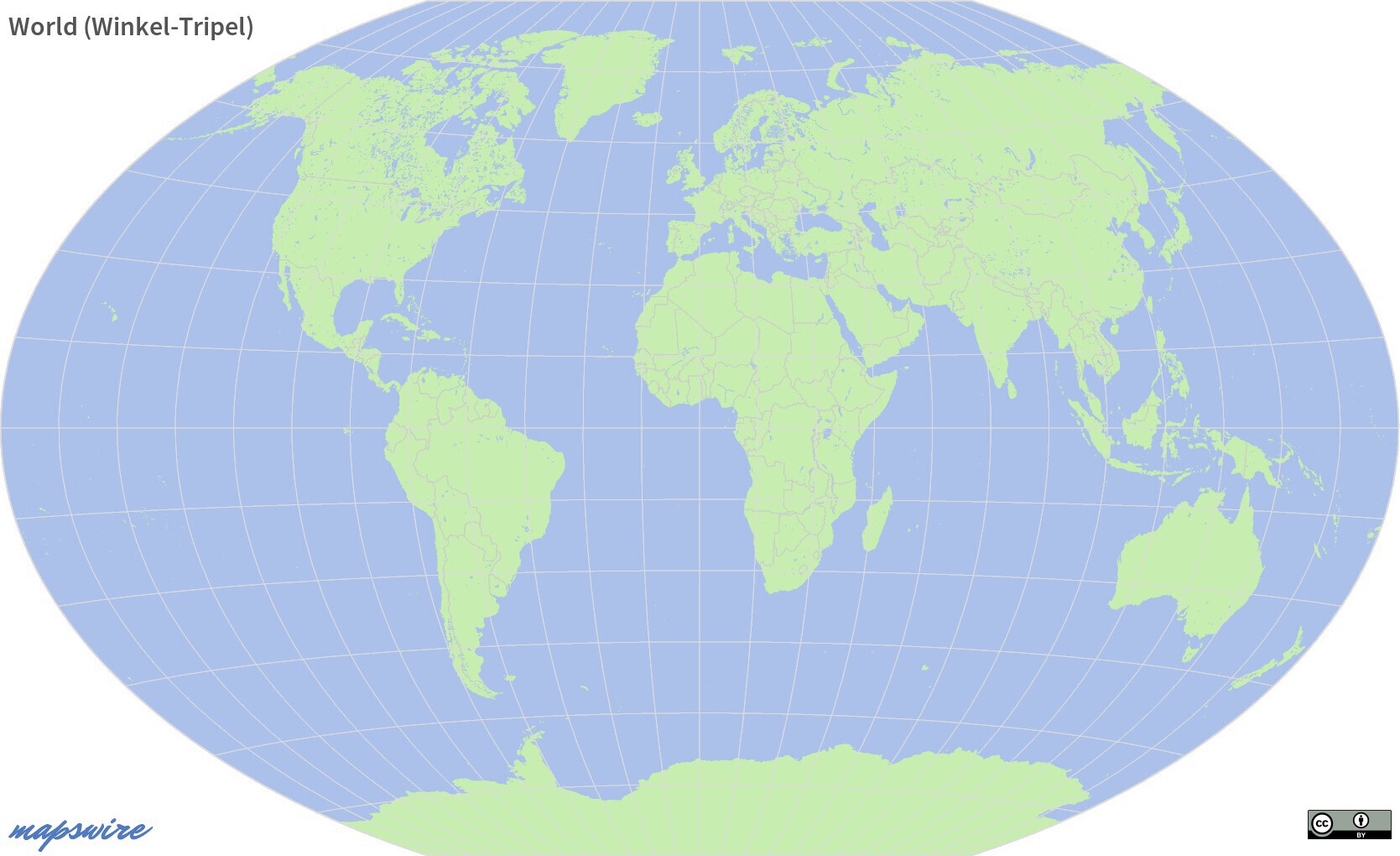
Winkel Tripel Projection
Looking somewhat similar to the Robinson and Mollweide projection, the Winkel Tripel projection is a compromise projection trying to reduce different distortions and works very well for world maps. In 1998 the National Geographic Society started to use Winkel Tripel as its standard projection for global maps.
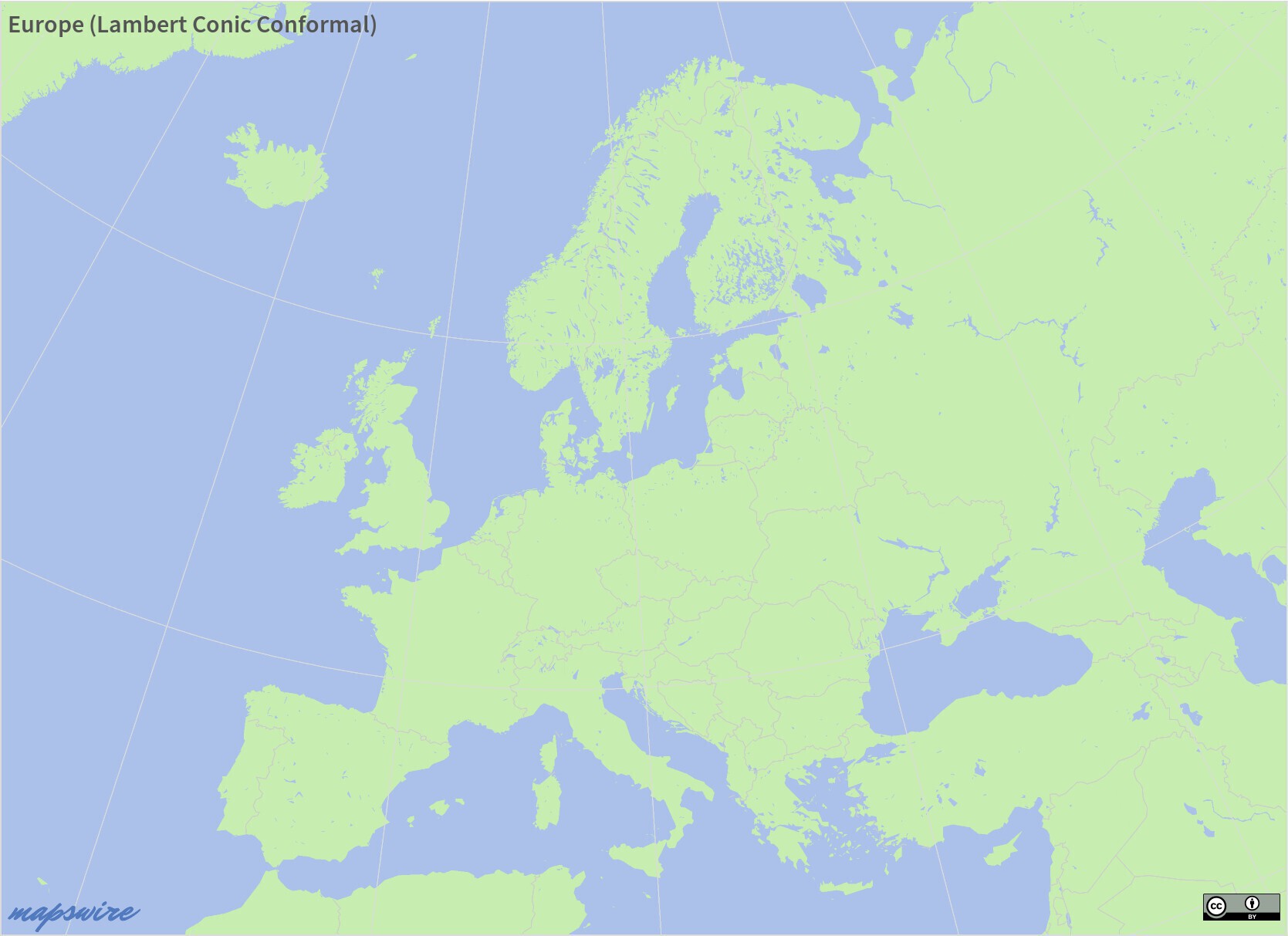
Lambert Conic Conformal Projection
This conformal projection is often used for medium scale maps of countries or continents. It doesn’t work well for world maps.